3) Proof by simulation — The Central Limit Theorem (CLT)

Data Simulation with Monte Carlo Methods

Marko Bachl

University of Hohenheim

Proof by simulation — The Central Limit Theorem (CLT)

Traktandenliste

1. Introduction & overview

2. Monte Carlo Simulation?

3. Proof by simulation — The Central Limit Theorem (CLT)

4. Errors and power — Torturing the t-test

5. Misclassification and bias — Messages mismeasured

6. Outlook: What’s next?

3. Proof by simulation — The CLT

1. Short intro (refresher): Getting Started with Randomness (in R)

2. “Proving” the Central Limit Theorem by simulation

Getting Started with Randomness (in R)

How to generate pseudo-random numbers

• Computers are deterministic machines and, by themselves alone, cannot create true random numbers.

• Pseudo-random number generators are used to create numbers which appear random according to a set of criteria.

• Long tradition of research in Computer Science, including work by John von Neumann.

• Pseudo-randomness is mostly considered a problem. But one advantage for simulation studies: Pseudo-random numbers are reproducible.

• For details in R, see ?RNG.

How to generate random numbers in R

• The {stats} package (comes with R) includes functions for working with many standard probability distributions, see ?Distributions for an overview.

• Functions are provided for density function, cumulative distribution function, quantile function and random number generation.

• They are named dxxx, pxxx, qxxx, and rxxx.

  • e.g., dnorm, pnorm, qnorm, and rnorm for the ?Normal distribution.

dnorm() - density of a normal distribution

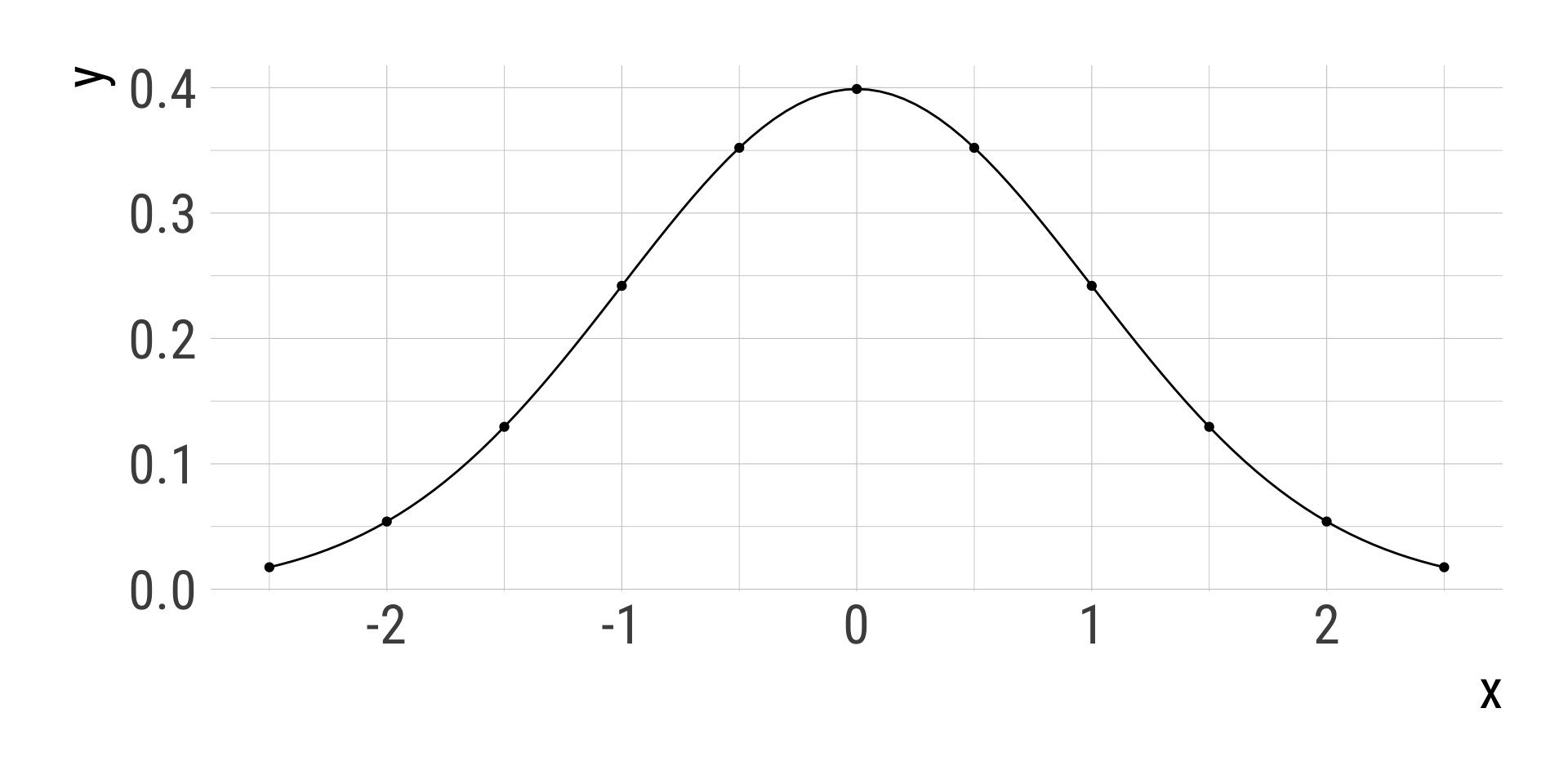
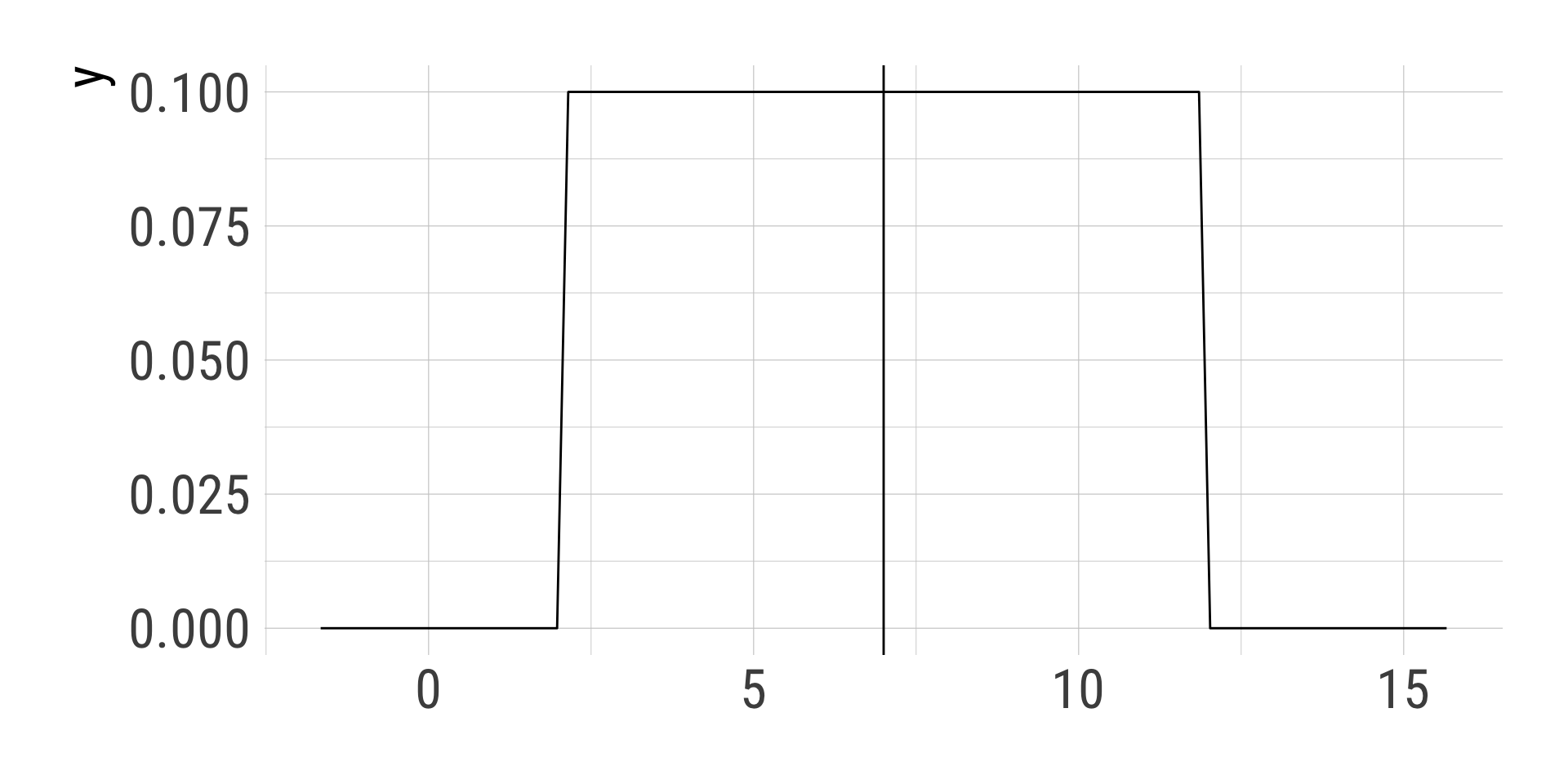
dnorm(x = 0, mean = 0, sd = 1, log = FALSE)

[1] 0.3989423

dnorm(x = seq(-2.5, 2.5, by = 0.5), mean = 0, sd = 1, log = FALSE)

 [1] 0.01752830 0.05399097 0.12951760 0.24197072 0.35206533 0.39894228
 [7] 0.35206533 0.24197072 0.12951760 0.05399097 0.01752830

dnorm() - density of a normal distribution

tibble(x = seq(-2.5, 2.5, by = 0.5), y = dnorm(x)) %>% 
  ggplot(aes(x, y)) + geom_point() + stat_function(fun = dnorm)

pnorm() - distribution function of a normal distribution

pnorm(q = 0, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)

[1] 0.5

Common use case: normal test statistics to p values

2 * (1 - pnorm(q = 1.96))

[1] 0.04999579

qnorm() - quantile function of a normal distribution

qnorm(p = 0.5, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)

[1] 0

Common use case: critical values for normal test statistics (e.g., for confidence interval construction)

qnorm(p = c(0.025, 0.975), mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)

[1] -1.959964  1.959964

rnorm() - draw random numbers from a normal distribution

rnorm(n = 10, mean = 0, sd = 1)

 [1]  0.1285479  0.3013488 -0.2675520 -0.7283270 -0.4823082 -0.4022703
 [7]  1.1053333  2.0805185 -0.1295265  1.1362721

rnorm(n = 10, mean = 0, sd = 1)

 [1]  0.3698740 -1.8249175  0.1501437 -0.8489524 -1.0120649  2.1517843
 [7] -0.5111604 -0.3192509 -1.9702453  0.5959162

Always use set.seed() to make simulation results reproducible

set.seed(12)
(sim1 = rnorm(n = 10, mean = 0, sd = 1))

 [1] -1.4805676  1.5771695 -0.9567445 -0.9200052 -1.9976421 -0.2722960
 [7] -0.3153487 -0.6282552 -0.1064639  0.4280148

set.seed(12)
(sim2 = rnorm(n = 10, mean = 0, sd = 1))

 [1] -1.4805676  1.5771695 -0.9567445 -0.9200052 -1.9976421 -0.2722960
 [7] -0.3153487 -0.6282552 -0.1064639  0.4280148

sim1 == sim2

 [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE

• Be aware that seeds do not necessarily lead to the same results across different machines.

sample() draws a random sample from a vector

Vector with 6 elements

LETTERS[1:6]

[1] "A" "B" "C" "D" "E" "F"

Sample 3 elements without replacement, equal sampling probabilities

sample(x = LETTERS[1:6], size = 3, replace = FALSE, prob = NULL)

[1] "E" "D" "F"

Sample 3 elements with replacement, different sampling probabilities

sample(x = LETTERS[1:6], size = 3, replace = TRUE, prob = 1:6)

[1] "E" "F" "E"

sample() can do many useful things

• The default for size is length(x).

Random permutation: Sample 6 out 6 elements without replacement

sample(x = LETTERS[1:6])

[1] "B" "C" "F" "A" "E" "D"

Bootstrapping: Sample 6 elements with replacement

sample(x = LETTERS[1:6], replace = TRUE)

[1] "D" "E" "E" "A" "B" "F"

Questions?

“Proving” the Central Limit Theorem by simulation

Pop quiz: What’s the difference between a sample distribution and a sampling distribution?

The Central Limit Theorem (CLT)

Central Limit Theorem according to Wikipedia

CLT step-by-step

• There is a quantity with population mean \(\mu\) and population standard deviation \(\sigma\).

• We repeatedly draw samples of size \(n\) from the population.

• We compute the sample mean \(\hat{\mu}\) of the quantity for each sample.

• The means will have a normal distribution, \(\sf{Normal}(\mu, \frac{\sigma}{\sqrt{n}})\).

• This holds regardless of the distribution of the quantity in the population (if the distribution has finite variance).

• But is this really true?

Analytical proof of the CLT

Analytical proof according to Wikipedia

Proof by simulation

• There is a quantity with population mean \(\mu\) and population standard deviation \(\sigma\).

• Most simple example: The quantity is normally distributed in the population.

set.seed(436) # make results reproducible 
mu = 5
sigma = 3
ggplot() + 
  stat_function(fun = dnorm,
                args = list(mean = mu, sd = sigma),
                xlim = c(mu-3*sigma, mu+3*sigma))

Proof by simulation

• We repeatedly draw samples of size \(n\) from the population.

n = 100
(one_sim = rnorm(n = n, mean = mu, sd = sigma)) %>% round(2)

  [1]  8.99  3.01  0.93 11.51 11.86 -1.90  3.84  7.03  2.14  5.55  5.91  6.91
 [13]  8.82 11.83  2.92  4.44  5.38  5.77  5.41  2.08  0.71 10.02  4.42  9.70
 [25]  3.88  2.31  3.35  6.21  1.34  6.53  3.27  1.71  5.13  1.14  2.44  8.87
 [37]  4.29 -1.31  2.08  6.49  5.94  3.24  9.08  1.07  3.77  5.57  2.23  5.01
 [49]  5.00  6.67  5.73  3.45  3.47 10.22  3.44  8.23 10.06  4.90  9.24  5.30
 [61]  4.25  6.36  8.33  2.74  3.45  3.86 -0.37  9.06  8.85  8.65  5.19  1.78
 [73]  5.49  4.48  1.25  5.19  5.14  7.96  2.72 -0.83  5.07  6.64  6.51  4.32
 [85] -0.89  7.75  4.55  4.17 11.46  1.57  3.84  0.37  1.03  3.69  8.05 -0.83
 [97]  2.26  4.21  4.42  4.46

Proof by simulation

• We compute the sample mean \(\hat{\mu}\) of the quantity for each sample.

mean(one_sim)

[1] 4.828196

Proof by simulation

• If we want to do stuff repeatedly in R, we should use a function.

sim_CLT_normal = function(n, mu, sigma) {
  sims = rnorm(n = n, mean = mu, sd = sigma) # Draw sample
  mean(sims) # Compute mean
}
sim_CLT_normal(n = n, mu = mu, sigma = sigma)

[1] 5.217277

Proof by simulation

• And we call the function repeatedly with purrr::map().

i = 10000 # number of simulations
many_means = map_dbl(1:i, .f = ~ sim_CLT_normal(n = n, mu = mu, sigma = sigma))
many_means[1:20] %>% round(2)

 [1] 5.25 5.50 5.04 5.11 5.03 4.88 5.35 5.06 5.02 5.37 4.79 4.99 4.93 5.27 5.23
[16] 4.89 4.87 4.86 4.57 5.45

Proof by simulation

• The means will have a normal distribution, \(\sf{Normal}(\mu, \frac{\sigma}{\sqrt{n}})\).

mu; mean(many_means)

[1] 5

[1] 5.002684

sigma / sqrt(n); sd(many_means)

[1] 0.3

[1] 0.2992968

Proof by simulation

• The means will have a normal distribution, \(\sf{Normal}(\mu, \frac{\sigma}{\sqrt{n}})\).

Show the code

d_many_means = tibble(sim = 1:i, mu_hat = many_means)
d_many_means %>% 
  ggplot(aes(mu_hat)) + geom_histogram() + 
  geom_vline(xintercept = c(mu - sigma / sqrt(n), mu, mu + sigma / sqrt(n))) +
  geom_vline(xintercept = c(mean(many_means)-sd(many_means),
                            mean(many_means),
                            mean(many_means)+sd(many_means)), 
             color = "red", linetype = 2)
d_many_means %>% 
  ggplot(aes(sample = many_means)) +
  geom_qq(distribution = qnorm,
          dparams = c(mean = mu, sd = sigma / sqrt(n)), 
          geom = "line") + 
  geom_abline(slope = 1)

Histogram of sample means

Q-Q-Plot

Proof by simulation

• This holds regardless of the distribution of the quantity in the population (if the distribution has finite variance).

• Let’s check for a uniform distribution.

set.seed(89) # make results reproducible 
lower = 2 # lower bound of the uniform distribution
upper = 12 # upper bound of the uniform distribution
n = 100
mu = (lower + upper) / 2 # mean of a uniform distribution
sigma = sqrt(1/12 * (upper - lower)^2) # standard deviation of a uniform distribution
ggplot() + 
  stat_function(fun = dunif,
                args = list(min = lower, max = upper),
                xlim = c(mu-3*sigma, mu+3*sigma)) + 
  geom_vline(xintercept = mu) + labs(x = NULL)

Proof by simulation

• Simulation for a uniform distribution.

# new function
sim_CLT_uniform = function(n, lower, upper) {
  sims = runif(n = n, min = lower, max = upper)
  mean(sims)
}
i = 10000
many_means = map_dbl(1:i, .f = ~ sim_CLT_uniform(n = n, lower = lower, upper = upper))

Proof by simulation

• The CLT also holds for a uniform distribution.

mu; mean(many_means)

[1] 7

[1] 6.998775

sigma / sqrt(n); sd(many_means)

[1] 0.2886751

[1] 0.2890647

Proof by simulation

• The CLT also holds for a uniform distribution.

Show the code

d_many_means = tibble(sim = 1:i, mu_hat = many_means)
d_many_means %>% 
  ggplot(aes(mu_hat)) + geom_histogram() + 
  geom_vline(xintercept = c(mu - sigma / sqrt(n), mu, mu + sigma / sqrt(n))) +
  geom_vline(xintercept = c(mean(many_means)-sd(many_means),
                            mean(many_means),
                            mean(many_means)+sd(many_means)), 
             color = "red", linetype = 2)
d_many_means %>% 
  ggplot(aes(sample = many_means)) +
  geom_qq(distribution = qnorm, 
          dparams = c(mean = mu, sd = sigma / sqrt(n)),
          geom = "line") + 
  geom_abline(slope = 1)

Histogram of sample means

Q-Q-Plot

Proof by simulation

• This holds regardless of the distribution of the quantity in the population (if the distribution has finite variance).

• And for a discrete distribution? Let’s check for a binomial.

set.seed(357) # make results reproducible 
prob_one = 0.4 # Probability of a success (1, not 0)
n = 100
mu = prob_one # Because of CLT ;)
sigma = sqrt(prob_one * (1 - prob_one)) # Standard deviation of a binomial distribution
ggplot() + 
  stat_function(fun = dbinom,
                args = list(size = 1, prob = prob_one),
                xlim = c(0, 1),
                n = 2,
                geom = "bar") + 
  geom_vline(xintercept = mu) + labs(x = NULL)

Proof by simulation

• Simulation for a binomial distribution.

sim_CLT_binom = function(n, prob_one) {
  sims = rbinom(n = n, size = 1, prob = prob_one)
  mean(sims) # mean = prop(1)
}
i = 10000
many_means = map_dbl(1:i, .f = ~ sim_CLT_binom(n = n, prob_one = prob_one))

Proof by simulation

• The CLT holds again.

mu; mean(many_means)

[1] 0.4

[1] 0.400484

sigma / sqrt(n); sd(many_means)

[1] 0.04898979

[1] 0.04901026

Proof by simulation

• The CLT holds again.

Show the code

d_many_means = tibble(sim = 1:i, mu_hat = many_means)
d_many_means %>% 
  ggplot(aes(mu_hat)) + geom_histogram() + 
  geom_vline(xintercept = c(mu - sigma / sqrt(n), mu, mu + sigma / sqrt(n))) +
  geom_vline(xintercept = c(mean(many_means)-sd(many_means),
                            mean(many_means),
                            mean(many_means)+sd(many_means)), 
             color = "red", linetype = 2)
d_many_means %>% 
  ggplot(aes(sample = many_means)) +
  geom_qq(distribution = qnorm, 
          dparams = c(mean = mu, sd = sigma / sqrt(n)),
          geom = "line") + 
  geom_abline(slope = 1)

Histogram of sample means

Q-Q-Plot

General lessons for simulation studies

Conceptual points: 5 questions for Monte Carlo simulation studies

1. Question: What is the goal of the simulation?

   • Will the CLT hold for different population distributions?

2. Quantities of interest: What is measured in the simulation?

   • Mean and standard deviation of the sampling distribution

3. Evaluation strategy: How are the quantities assessed?

   • Comparison with population mean and analytical sampling distribution

4. Conditions: Which characteristics of the data generating model will be varied?

   • Different (types of) population distributions.

5. Data generating model: How are the data simulated?

   • Random draws from different distribtions with fixed sample sizes and moments.

General lessons for simulation studies

Practical points (in R)

• How to generate pseudo-random data

• How to use functions for things we want to do repeatedly.

• How to use purrr:map() to do things repeatedly.

• How to summarize data from simulation experiments.

Group exercise 1

Exercise 1a. Proving the CLT for a Poisson distribution

• Adapt the code from the examples to check whether the CLT also holds for a Poisson distribution.

  • Random numbers are sampled with rpois(n, lambda), where n is the sample size and lambda is the mean (and also the variance) of the distribution.

  • The population standard deviation is \(\sqrt{\lambda}\).

Exercise 1b. Proving the CLT for any other suitable distribution

• Select another suitable distribution from ?Distributions

  • Read the documentation to understand which arguments must be provided.

  • Find the definition of the population distribution’s standard deviation to calculate the analytical standard deviation of the sampling distribution.

  • Adapt the simulation and analysis code accordingly.