5) Misclassification and bias — Messages mismeasured

Data Simulation with Monte Carlo Methods

Marko Bachl

University of Hohenheim

Misclassification and bias — Messages mismeasured

Traktandenliste

1. Introduction & overview

2. Monte Carlo Simulation?

3. Proof by simulation — The Central Limit Theorem (CLT)

4. Errors and power — Torturing the t-test

5. Misclassification and bias — Messages mismeasured

6. Outlook: What’s next?

5. Misclassification and bias — Messages mismeasured

1. Univariate analysis of the misclassified variable

2. Misclassified variables as predictors

Misclassification

• Misclassification: Measurement error in categorical variables

• Units are assigned the “wrong” category.

• Important, but often ignored issue in (computational and human) content analysis:

  • Biased estimates

  • Reduced power of statistical tests

Misclassification

• Can be expressed as misclassification or confusion matrix:

\[ \Theta_A = \begin{pmatrix} \theta_{1|1} & \theta_{1|2} & \theta_{1|\dots} & \theta_{1|k} \\ \theta_{2|1} & \theta_{2|2} & \theta_{2|\dots} & \theta_{2|k} \\ \theta_{\dots|1} & \theta_{\dots|2} & \theta_{\dots|\dots} & \theta_{\dots|k} \\ \theta_{k|1} & \theta_{k|2} & \theta_{k|\dots} & \theta_{k|k} \end{pmatrix} \]

• Probability that each category is assigned given the true category.

• Columns sum to 1

First simulation study: Univariate analysis

1. Question: What is the goal of the simulation?

   • Understand how misclassification error affects the estimated proportions of a misclassified variable

2. Quantities of interest: What is measured in the simulation?

   • Deviation of proportion estimates from known population proportions

3. Evaluation strategy: How are the quantities assessed?

   • Inspection of the deviation for fixed population configurations
   • Root mean squared error (RMSE) for general analysis.

4. Conditions: Which characteristics of the data generating model will be varied?

   • Accuracy of the classification; Population distributions.

5. Data generating model: How are the data simulated?

   • Random draws from a categorical distribution; subsequent misclassification of the sampled units.

Practical considerations

• How to (somewhat efficiently) implement misclassification?

• How to evaluate the deviation of estimates from population values?

• How to sample population distributions from a \(\sf{Dirichlet}\) distribution?

• How to implement a randomly sampled factor in the simulation?

Two steps of the data generating process

1. Sample units from population

2. Measure variable with misclassification error

One simulation: Population

set.seed(28)
pop_dist = c(0.55, 0.3, 0.1, 0.05)
k = length(pop_dist) # number of categories
categories = LETTERS[1:k] # names of the categories
names(pop_dist) = categories
pop_dist

   A    B    C    D 
0.55 0.30 0.10 0.05 

One simulation: Sample

n = 1000 # sample size
sample_true = sample(x = categories, 
                     size = n, 
                     replace = TRUE, 
                     prob = pop_dist) %>% 
  factor(levels = categories) %>% # if any categories not observed in the sample
  sort() # important later for efficient misclassification
freq_true = sample_true %>% 
  table() %>% 
  prop.table()
freq_true

.
    A     B     C     D 
0.563 0.307 0.085 0.045 

One simulation: Misclassification matrix

# Simple: Equal error rates, equal difficulties, one process
accuracy = 0.8
equal_error = (1 - accuracy) / (k - 1)
misclass_prob = matrix(equal_error, nrow = k, ncol = k, 
                       dimnames = list(categories, categories))
diag(misclass_prob) = accuracy
misclass_prob

           A          B          C          D
A 0.80000000 0.06666667 0.06666667 0.06666667
B 0.06666667 0.80000000 0.06666667 0.06666667
C 0.06666667 0.06666667 0.80000000 0.06666667
D 0.06666667 0.06666667 0.06666667 0.80000000

One simulation: Misclassification

First try

• Mimic empirical classification process at unit level

tic()
sample_obs = sample_true %>%  # n samples
  map_chr(~ sample(categories,
                  size = 1, replace = FALSE, 
                  prob = misclass_prob[, .x])) %>%
    factor(levels = categories)
freq_obs = sample_obs %>% 
    table() %>% 
    prop.table()
toc()

0.017 sec elapsed

freq_obs

.
    A     B     C     D 
0.483 0.293 0.138 0.086 

One simulation: Misclassification

Second try

• Less computational costs at the at category level

tic()
sample_obs = table(sample_true) %>%  # k samples
  imap(~ sample(categories,
                  size = .x, replace = TRUE, 
                  prob = misclass_prob[, .y])) %>%
    unlist(use.names = FALSE) %>% 
    factor(levels = categories)
freq_obs = sample_obs %>% 
  table() %>% 
    prop.table()
toc()

0.003 sec elapsed

freq_obs

.
    A     B     C     D 
0.496 0.299 0.128 0.077 

One simulation: Quantification of error

Root mean squared error (RMSE); but which reference?

• Error due to sampling and misclassification compared to population

sqrt(mean((pop_dist - freq_obs)^2)) %>% round(2)

[1] 0.03

• Error due to misclassification compared to true values in sample

sqrt(mean((freq_true - freq_obs)^2)) %>% round(2)

[1] 0.04

• (Error due to sampling compared to population)

sqrt(mean((pop_dist - freq_true)^2)) %>% round(2)

[1] 0.01

Wrap it into a function

sim_misclass = function(pop_dist = c(0.55, 0.3, 0.1, 0.05),
                        n = 1000,
                        accuracy = 0.8) {
  # Population
  k = length(pop_dist)
  categories = LETTERS[1:k]
  
  # Sample
  sample_true = sample(x = categories, 
                       size = n, 
                       replace = TRUE, 
                       prob = pop_dist) %>% 
    factor(levels = categories) %>% 
    sort()
  freq_true = sample_true %>% 
    table() %>% 
    prop.table()
  
  # Misclassification
  equal_error = (1 - accuracy) / (k - 1)
  misclass_prob = matrix(equal_error, nrow = k, ncol = k,
                         dimnames = list(categories, categories))
  diag(misclass_prob) = accuracy

  sample_obs = table(sample_true) %>%  
    imap(~ sample(categories,
                  size = .x, replace = TRUE, 
                  prob = misclass_prob[, .y])) %>%
    unlist(use.names = FALSE) %>% 
    factor(levels = categories)
  freq_obs = sample_obs %>% 
    table() %>% 
    prop.table()

  # Error summary
  rmse = sqrt(mean((pop_dist - freq_obs)^2))

  # Output
  out = lst(freq_true, freq_obs, rmse)
  out
}

Experimental conditions

• pop_dist must be wrapped into another list, because the condition is defined by the vector of proportions.

• n (sample size) fixed.

• Between-simulation factor: accuracy.

conditions = expand_grid(
  pop_dist = list(c(0.55, 0.3, 0.1, 0.05)),
  n = 1000,
  accuracy = seq(from = 0.4, to = 1, by = 0.1)
  ) %>% 
  rowid_to_column(var = "condition")
conditions

# A tibble: 7 × 4
  condition pop_dist      n accuracy
      <int> <list>    <dbl>    <dbl>
1         1 <dbl [4]>  1000      0.4
2         2 <dbl [4]>  1000      0.5
3         3 <dbl [4]>  1000      0.6
4         4 <dbl [4]>  1000      0.7
5         5 <dbl [4]>  1000      0.8
6         6 <dbl [4]>  1000      0.9
7         7 <dbl [4]>  1000      1  

Run simulation experiment

i = 1000 # less simulations to save some workshop time 
set.seed(39)
tic()
sims = map_dfr(1:i, ~ conditions) %>%
  rowid_to_column(var = "sim") %>%
  rowwise() %>%
  mutate(res = list(sim_misclass(pop_dist = pop_dist, 
                                 n = n, accuracy = accuracy)))
toc()

5.099 sec elapsed

Results: Proportion estimates

Show the code

sims %>% 
  ungroup() %>% 
  unnest_wider(res) %>% 
  unnest_longer(freq_obs, indices_to = "category") %>% 
  group_by(accuracy, category) %>% 
  summarise(Q = list(quantile(freq_obs, probs = c(0.25, 0.5, 0.75)))) %>% 
  unnest_wider(Q) %>% 
  ggplot(aes(`50%`, factor(accuracy), 
             xmin = `25%`, xmax = `75%`, color = category)) +
  geom_pointrange() +
  labs(x = str_glue("Median and IQR of the proportions from {i} simulation runs per condition."),
       y = "accuracy")

Results: RMSE

Show the code

sims %>% 
  ungroup() %>% 
  unnest_wider(res) %>% 
  group_by(accuracy) %>% 
  summarise(Q = list(quantile(rmse, probs = c(0.25, 0.5, 0.75)))) %>% 
  unnest_wider(Q) %>% 
  ggplot(aes(accuracy, `50%`, ymin = `25%`, ymax = `75%`)) + 
  geom_pointrange() + 
  geom_line() +
  labs(y = "RMSE (Mdn & IQR)",
       x = "accuracy")

Summary

• Bias towards \(1/k\).

• Less accuracy, stronger bias. Substantial bias even with seemingly sufficient accuracy.

• Stronger bias for categories which are farther from \(1/k\).

• Implies: More uneven distributions, stronger bias — but how much?

Adjust experimental conditions

• Add varying population distributions - but how?

• One possible solution: Factor of different distributions, e.g.,

list(pd1 = c(0.25, 0.25, 0.25, 0.25), 
     pd2 = c(0.55, 0.30, 0.10, 0.05))

• Another possibility: Sample from a distribution of population distributions.

rdirichlet(n = 3, alpha = c(1,1,1,1)) %>% round(2)

     [,1] [,2] [,3] [,4]
[1,] 0.26 0.54 0.19 0.01
[2,] 0.59 0.37 0.04 0.00
[3,] 0.19 0.50 0.22 0.09

Adjust experimental conditions

• Only accuracy is varied between conditions.

• pop_dist is sampled from rdirichlet(alpha = c(1,1,1,1)) for each simulation run.

• i (number of simulations) and set.seed() required for building conditions.

i = 5000
set.seed(39)
conditions = expand_grid(
  n = 1000,
  accuracy = seq(from = 0.4, to = 1, by = 0.2)
  ) %>% 
  rowid_to_column(var = "condition")
conditions = map_dfr(1:i, ~ conditions) %>%
  rowid_to_column(var = "sim") %>%
  mutate(pop_dist = split(rdirichlet(nrow(.), c(1,1,1,1)), 1:nrow(.)))
conditions

# A tibble: 20,000 × 5
     sim condition     n accuracy pop_dist    
   <int>     <int> <dbl>    <dbl> <named list>
 1     1         1  1000      0.4 <dbl [4]>   
 2     2         2  1000      0.6 <dbl [4]>   
 3     3         3  1000      0.8 <dbl [4]>   
 4     4         4  1000      1   <dbl [4]>   
 5     5         1  1000      0.4 <dbl [4]>   
 6     6         2  1000      0.6 <dbl [4]>   
 7     7         3  1000      0.8 <dbl [4]>   
 8     8         4  1000      1   <dbl [4]>   
 9     9         1  1000      0.4 <dbl [4]>   
10    10         2  1000      0.6 <dbl [4]>   
# … with 19,990 more rows
# ℹ Use `print(n = ...)` to see more rows

Run simulation experiment

tic()
sims = conditions %>% 
  rowwise() %>%
  mutate(res = list(sim_misclass(pop_dist = pop_dist, n = n, accuracy = accuracy)))
toc()

14.592 sec elapsed

Measure for population distribution variation

• \(\chi^2\) value of the standardized (proportions * 100, independent from n) distribution.

sims %>% 
  ungroup() %>% 
  unnest_wider(res) %>% 
  mutate(chi2_pop_dist = map_dbl(pop_dist, ~ chisq.test(.x*100)$statistic)) %>% 
  ggplot(aes(chi2_pop_dist)) +
  geom_histogram()

Results

Show the code

sims %>% 
  ungroup() %>% 
  unnest_wider(res) %>% 
  mutate(chi2_pop_dist = map_dbl(pop_dist, ~ chisq.test(.x*100)$statistic)) %>% 
  ggplot(aes(chi2_pop_dist, rmse, color = factor(accuracy))) +
  geom_smooth() +
  xlim(0, 155) +
  labs(x = "chi2_pop_dist",
       color = "accuracy",
       y = "RMSE",
       caption = "method = 'gam' and formula 'y ~ s(x, bs = 'cs')")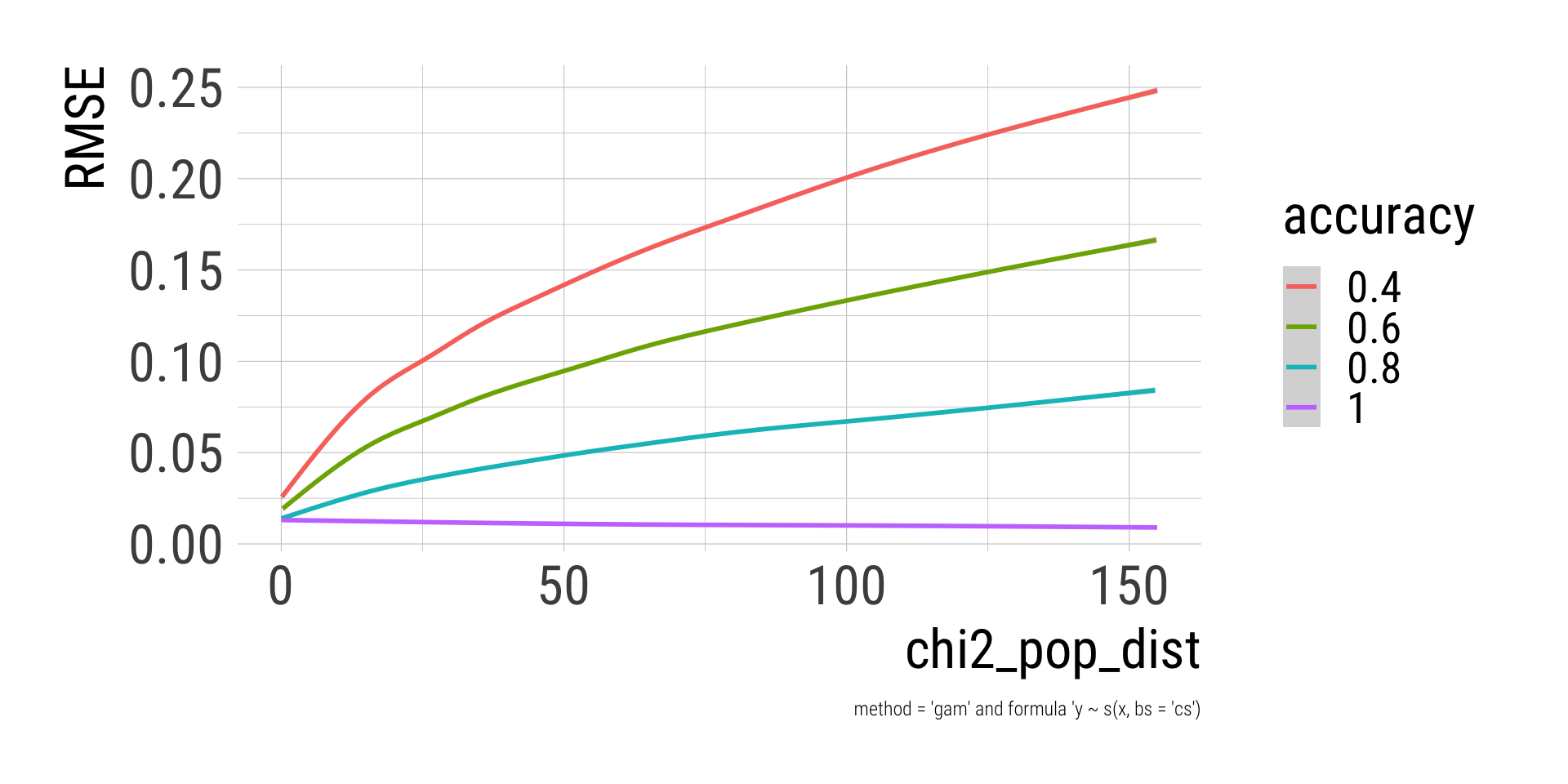

Show the code

sims %>% 
  ungroup() %>% 
  unnest_wider(res) %>% 
  mutate(chi2_pop_dist = map_dbl(pop_dist, ~ chisq.test(.x*100)$statistic)) %>% 
  filter(round(chi2_pop_dist) %in% c(0, 25, 50, 75, 100, 125, 150)) %>% 
  group_by(round(chi2_pop_dist)) %>% 
  slice(1) %>% 
  ungroup() %>% 
  arrange(chi2_pop_dist) %>% 
  select(chi2_pop_dist, pop_dist) %>% 
  mutate(pop_dist = map(pop_dist, sort, decreasing = TRUE)) %>% 
  unnest_wider(pop_dist) %>% 
  kable(digits = 2, col.names = c("chi2_pop_dist", LETTERS[1:4]))

chi2_pop_dist	A	B	C	D
0.11	0.26	0.26	0.25	0.24
24.58	0.40	0.34	0.14	0.12
50.27	0.53	0.25	0.15	0.06
74.82	0.62	0.17	0.12	0.09
99.68	0.68	0.16	0.10	0.06
124.52	0.73	0.13	0.07	0.06
150.11	0.77	0.16	0.04	0.03

Summary: Substantial conclusion

• Deviation of the populations distribution from equal proportions is strongly related to error magnitude, such that more unequal proportions are estimated less accurate.

• There seems to be a non-linear interaction between population distribution and accuracy, such that the consequences of lesser accuracy are more severe for more unequal distribution.

Summary: For simulation experiments

• Assignment of random values at each simulation run as an alternative

• Also an option for accuracy (runif(min = 0.4, 1.0)) or sample size (sample(x = 300:2000, replace = TRUE), see Section 4)

• Most helpful if we want to look at an outcome across the whole range of values. Not so helpful if discretized after the simulation.

Questions?

Misclassification and bias — Messages mismeasured

5. Misclassification and bias — Messages mismeasured

1. Univariate analysis of the misclassified variable

2. Misclassified variables as predictors

Second simulation study: Misclassified predictors

1. Question: What is the goal of the simulation?

   • How does misclassification error affect the estimated differences in an outcome and the statistical power to detect these differences if the grouping variable is misclassified?

2. Quantities of interest: What is measured in the simulation?

   • Observed group differences and their ratios to the true group differences

   • Statistical power to detect the difference with \(p < .05\) in Welch’s t-test

3. Evaluation strategy: How are the quantities assessed?

   • Inspection of the deviation between true and observed differences and their ratios across conditions

   • Comparison of statistical power to reject the Null hypothesis if the alternative hypothesis is true

4. Conditions: Which characteristics of the data generating model will be varied?

   • Accuracy of the classification; within-group variances

5. Data generating model: How are the data simulated?

   • Grouping variable: Random draws from a categorical distribution; subsequent misclassification of the sampled units

   • Outcome: Random draws from Poisson distributions with different \(\lambda\) values

Three steps of the data generating process

1. Sample units from population

2. Measure variable with misclassification error

3. Sample outcome from population

One simulation: Population grouping variable

Same as before

set.seed(4026)
pop_dist = c(0.55, 0.3, 0.1, 0.05)
k = length(pop_dist) # number of categories
categories = LETTERS[1:k] # names of the categories
names(pop_dist) = categories
pop_dist

   A    B    C    D 
0.55 0.30 0.10 0.05 

One simulation: Sample grouping variable

Same as before

n = 1000 # sample size
sample_true = sample(x = categories, 
                     size = n, 
                     replace = TRUE, 
                     prob = pop_dist) %>% 
  factor(levels = categories) %>% # if any categories not observed in the sample
  sort() # important later for efficient misclassification
freq_true = sample_true %>% 
  table() %>% 
  prop.table()
freq_true

.
    A     B     C     D 
0.568 0.290 0.100 0.042 

One simulation: Sample outcome

lambdas = c(21:24)
names(lambdas) = categories
outcomes = table(sample_true) %>% 
  imap(~ rpois(n = .x, lambda = lambdas[.y])) %>% 
  unlist(use.names = FALSE)
table(sample_true, outcomes)

           outcomes
sample_true  8 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
          A  1  2  8  4  7 16 24 33 41 36 43 56 50 39 44 59 28 24 17 12  9  6
          B  0  0  0  0  7  7  8 12 14 16 22 19 19 30 27 20 19 16 17  8  6  9
          C  0  0  0  0  2  3  2  3  6  2  8  6  4  6  7  7  6  5  7  6 10  2
          D  0  0  0  0  0  0  1  1  4  1  2  2  2  4  2  4  3  4  4  3  1  1
           outcomes
sample_true 31 32 33 34 35 42
          A  2  2  2  2  0  1
          B  7  0  2  4  1  0
          C  3  2  3  0  0  0
          D  1  0  1  1  0  0

One simulation: Misclassification matrix

Same as before

# Simple: Equal error rates, equal difficulties, one process
accuracy = 0.8
equal_error = (1 - accuracy) / (k - 1)
misclass_prob = matrix(equal_error, nrow = k, ncol = k, 
                       dimnames = list(categories, categories))
diag(misclass_prob) = accuracy
misclass_prob

           A          B          C          D
A 0.80000000 0.06666667 0.06666667 0.06666667
B 0.06666667 0.80000000 0.06666667 0.06666667
C 0.06666667 0.06666667 0.80000000 0.06666667
D 0.06666667 0.06666667 0.06666667 0.80000000

One simulation: Misclassification

Same as before

tic()
sample_obs = table(sample_true) %>%  # k samples
  imap(~ sample(categories,
                  size = .x, replace = TRUE, 
                  prob = misclass_prob[, .y])) %>%
    unlist(use.names = FALSE) %>% 
    factor(levels = categories)
freq_obs = sample_obs %>% 
  table() %>% 
    prop.table()
toc()

0.003 sec elapsed

freq_obs

.
    A     B     C     D 
0.476 0.287 0.142 0.095 

One simulation: Measure quantities of interest

• Test means of outcome in categories B, C, and D against A (the default)

t_res = categories[2:k] %>% 
  map(~ t.test(outcomes[sample_obs == "A"],
               outcomes[sample_obs == .x])) %>% 
  set_names(str_c("A_", categories[2:k]))

 

• Extract group mean differences

t_res %>% 
  map_dbl(~ diff(.x$estimate)) %>% round(2)

 A_B  A_C  A_D 
1.00 1.54 0.66 

• Extract p-values

t_res %>% 
  map_dbl(~ .x$p.value) %>% round(5)

    A_B     A_C     A_D 
0.00520 0.00081 0.21381 

Wrap it into a function

sim_misclass_test = function(pop_dist = c(0.55, 0.3, 0.1, 0.05),
                        lambdas = c(3:6),
                        n = 1000,
                        accuracy = 0.8) {
  # Population
  k = length(pop_dist)
  categories = LETTERS[1:k]
  names(lambdas) = categories
  
  # True sample
  sample_true = sample(x = categories, 
                       size = n, 
                       replace = TRUE, 
                       prob = pop_dist) %>% 
    factor(levels = categories) %>% 
    sort()
  freq_true = sample_true %>% 
    table() %>% 
    prop.table()
  outcomes = table(sample_true) %>% 
    imap(~ rpois(n = .x, lambda = lambdas[.y])) %>% 
    unlist(use.names = FALSE)

  # Misclassification probabilities
  equal_error = (1 - accuracy) / (k - 1)
  misclass_prob = matrix(equal_error, nrow = k, ncol = k, 
                         dimnames = list(categories, categories))
  diag(misclass_prob) = accuracy
  
  # Misclassification  
  sample_obs = table(sample_true) %>%  
    imap(~ sample(categories,
                  size = .x, replace = TRUE, 
                  prob = misclass_prob[, .y])) %>%
    unlist(use.names = FALSE) %>% 
    factor(levels = categories)
  freq_obs = sample_obs %>% 
    table() %>% 
    prop.table()
  
  # Model
  ttests_obs = categories[2:k] %>% 
    map(~ t.test(outcomes[sample_obs == "A"],
                 outcomes[sample_obs == .x])) %>% 
    set_names(str_c("A_", categories[2:k]))

  # Error summary for categories
  rmse = sqrt(mean((pop_dist - freq_obs)^2))

  # Output
  out = lst(freq_true, freq_obs, rmse,
            p_obs = ttests_obs %>% 
              map_dbl(~ .x$p.value),
            diff_obs = ttests_obs %>% 
              map_dbl(~ diff(.x$estimate))
            )
  out
}

Experimental conditions

• lambdas is a named list with two sets of values. The group differences are the same in both conditions, but the variances differ strongly.

• Between-simulation factor: accuracy varies with 4 values.

• pop_dist and n (sample size) are fixed.

conditions = expand_grid(
  pop_dist = list(c(0.55, 0.3, 0.1, 0.05)),
  lambdas = list(start_1 = c(1:4),
                 start_21 = c(21:24)),
  n = 1000,
  accuracy = seq(from = 0.4, to = 1, by = 0.2)
) %>% 
  rowid_to_column(var = "condition")
conditions

# A tibble: 8 × 5
  condition pop_dist  lambdas          n accuracy
      <int> <list>    <named list> <dbl>    <dbl>
1         1 <dbl [4]> <int [4]>     1000      0.4
2         2 <dbl [4]> <int [4]>     1000      0.6
3         3 <dbl [4]> <int [4]>     1000      0.8
4         4 <dbl [4]> <int [4]>     1000      1  
5         5 <dbl [4]> <int [4]>     1000      0.4
6         6 <dbl [4]> <int [4]>     1000      0.6
7         7 <dbl [4]> <int [4]>     1000      0.8
8         8 <dbl [4]> <int [4]>     1000      1  

Run simulation experiment

i = 1000
set.seed(39)
tic()
sims = map_dfr(1:i, ~ conditions) %>%
  rowid_to_column(var = "sim") %>%
  rowwise() %>%
  mutate(res = list(sim_misclass_test(
    pop_dist = pop_dist,
    lambdas = lambdas, 
    n = n, accuracy = accuracy)))
toc()

13.79 sec elapsed

Results: Estimated differences

Show the code

sims %>% 
  ungroup() %>% 
  unnest_wider(res) %>% 
  unnest_longer(diff_obs, indices_to = "difference") %>% 
  mutate(lambdas = names(lambdas)) %>% 
  group_by(accuracy, difference, lambdas) %>% 
  summarise(Q = list(quantile(diff_obs, probs = c(0.25, 0.5, 0.75)))) %>% 
  unnest_wider(Q) %>% 
  ggplot(aes(`50%`, factor(accuracy),
             xmin = `25%`, xmax = `75%`, color = difference)) +
  geom_pointrange() +
  facet_wrap(vars(lambdas)) + 
  labs(y = "accuracy",
       x = str_glue("Median and IQR of the mean differences from {i} simulation runs per condition."))

Results: Ratio estimated to true differences

Show the code

sims %>% 
  ungroup() %>% 
  unnest_wider(res) %>% 
  unnest_longer(diff_obs, indices_to = "difference") %>% 
  mutate(
    diff_true = case_when(
      difference == "A_B" ~ 1L,
      difference == "A_C" ~ 2L,
      difference == "A_D" ~ 3L
    ),
    recovered = diff_obs / diff_true,
    lambdas = names(lambdas)
    ) %>% 
  select(accuracy, difference, lambdas, diff_obs, diff_true, recovered) %>% 
  group_by(accuracy, difference, lambdas) %>% 
  summarise(Q = list(quantile(recovered, probs = c(0.25, 0.5, 0.75)))) %>% 
  unnest_wider(Q) %>% 
  ggplot(aes(`50%`, factor(accuracy),
             xmin = `25%`, xmax = `75%`, color = difference)) +
  geom_pointrange() +
  facet_wrap(vars(lambdas)) + 
  labs(y = "accuracy",
       x = str_glue("Median and IQR of the ratio true by observed difference\nfrom {i} simulation runs per condition."))

Results: Power

Show the code

sims %>% 
  ungroup() %>% 
  mutate(lambdas = names(lambdas)) %>% 
  unnest_wider(res) %>% 
  unnest_longer(p_obs, indices_to = "difference") %>% 
  group_by(accuracy, difference, lambdas) %>% 
  summarise(P_p05 = mean(p_obs < 0.05)) %>% 
  ggplot(aes(accuracy, P_p05, color = difference)) + 
  geom_point() + geom_line() +
  facet_wrap(vars(lambdas)) + 
  labs(y = "Power at p < .05")

Summary

• Misclassification of the grouping variable attenuates the group differences and reduces statistical power.

• Even a seemingly ok-ish accuracy of .8 can lead to a reduction of the observed differences to 50% of the true difference in some instances.

• The level of within-group variances obviously reduces statistical power, but does not seem to be related to the average bias of the observed differences.

Questions?

Group exercise 3

Group exercise 3

Try one (or more) of the following adaptions of the Monte Carlo studies on misclassification:

1. Change the first simulation so that the misclassification probabilities to allow for different patterns accuracies and errors: varying difficulties of the categories, systematic confusion of some categories.

2. Investigate the consequences of misclassification error for an analysis of two binary variables which were both measured with misclassification error.

Exercise 3a: Help

Expand if you need help.

Don’t expand if you want to figure it out by yourself.

Scroll down if you need more help on later steps.

Manually defined misclassification matrix with varying difficulty and systematic confusion

Code

misclass_prob = matrix(c(
  .80, .10, .15,
  .15, .80, .15,
  .05, .10, .70
), nrow = 3, byrow = TRUE,
dimnames = list(LETTERS[1:3], LETTERS[1:3]))
misclass_prob

Adapted simulation function

Code

# Misclassification matrix as argument
sim_misclass = function(pop_dist = c(0.55, 0.3, 0.1, 0.05),
                        n = 1000,
                        misclass_prob = misclass_prob) {
  # Population
  k = length(pop_dist)
  categories = LETTERS[1:k]
  
  # Sample
  sample_true = sample(x = categories, 
                       size = n, 
                       replace = TRUE, 
                       prob = pop_dist) %>% 
    factor(levels = categories) %>% 
    sort()
  freq_true = sample_true %>% 
    table() %>% 
    prop.table()
  
  # Misclassification
  sample_obs = table(sample_true) %>%  
    imap(~ sample(categories,
                  size = .x, replace = TRUE, 
                  prob = misclass_prob[, .y])) %>%
    unlist(use.names = FALSE) %>% 
    factor(levels = categories)
  freq_obs = sample_obs %>% 
    table() %>% 
    prop.table()
  
  # Error summary
  rmse = sqrt(mean((pop_dist - freq_obs)^2))
  
  # Output
  out = lst(freq_true, freq_obs, rmse)
  out
}

Condition

Code

# No experiment, just one condition for illustration
conditions = expand_grid(
  pop_dist = list(c(0.55, 0.3, 0.15)),
  n = 1000,
  misclass_prob = list(misclass_prob)
) %>% 
  rowid_to_column(var = "condition")
conditions

Run simulation

Code

i = 1000 # less simulations to save some workshop time 
set.seed(40)
tic()
sims = map_dfr(1:i, ~ conditions) %>%
  rowid_to_column(var = "sim") %>%
  rowwise() %>%
  mutate(res = list(sim_misclass(pop_dist = pop_dist, 
                                 n = n, misclass_prob = misclass_prob)))
toc()

Result plot

Code

sims %>% 
  ungroup() %>% 
  unnest_wider(res) %>% 
  unnest_longer(freq_obs, indices_to = "category") %>% 
  group_by(category) %>%
  summarise(Q = list(quantile(freq_obs, probs = c(0.25, 0.5, 0.75)))) %>%
  unnest_wider(Q) %>%
  ggplot(aes(`50%`, fct_rev(category),
             xmin = `25%`, xmax = `75%`)) +
  geom_pointrange() +
  geom_vline(xintercept = unlist(conditions$pop_dist), color = "red", linetype = 2) + 
  labs(x = str_glue("Median and IQR of the proportions from {i} simulation runs per condition.\nRed lines are shares in the population."),
       y = "Category")

Exercise 3b: Help

Check out the steps-by-step explanation in the rendered solution or the R code.